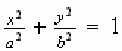
Ellipse

DEFINITION: "the set of points which sum of the distances between two given points known as foci (plural of focus) is costant" ;

 CONSIDERATIONS:

The point P belongs to the ellipse if, and only if, the distance between the point P from the focus F1 plus the distance of the point P from the focus F2 is costant, that is: PF1+PF2=k. If the point P which belongs to the ellipse has generic coordinates X and Y then the equation of the ellipse in the canonic form can be found, in case the two foci lie on the axis X or on the axis Y,it is:

((x²)/(a²))+((y²)/(b²))=1

where a is the measure of the semiaxis of the ellipse which lies on the axis X, while b is the measure of the semiaxis of the ellipse which lies on the axis Y. Because of the fact a and b are measures of segments then both a and b must be positive and if a is major of b then the ellipse has the major axis; called even focal axis because two foci lie on it, on the axis x, while if a is lesser of b then the major axis lies on the axis Y.

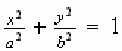
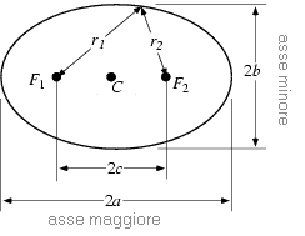
 to find the equation of the ellipse we must considerate the definition: let's take a generic point P(x,y) and let's impose that the sum of the distances of P from the two fixed points F1 (c,0) and F2 (-c,0) is equal to 2a;

PF1 + PF2 = 2a

1. I apply the formula of the distance between two points on the plain and I obtain;

2. It's an irrational equation so I must isolate one root;

3. I rise to the square both parts from the equal;

4. I sum the similar terms and isolate the root before the equal;

5. I divide all the terms for 4;

6. I rise to the square both parts;

7.I multiply a^2 to all the terms in brackets ;

8. Terms with the x and the y before of the equal, the others after the equal;

9. I eliminate two equal terms and of opposite sign;

10. I put in evidence x^2 before the equal and a^2 after the equal;

11. I put a^2 – c^2 = b^2 I can do it because a > c;

12. I divide the terms for a^2b^2;

13. I simplify and I obtain the canonical equation of the ellipse ;

 If the equation of the ellipse becomes:

a circumference of centre the origin and ray