GRUPPO DI LAVORO AMODEO DARIO, SCARAMOZZINO GIUSEPPE E ZAMINGA SAMUELE DI 3
 H E TRAPANI DOMENICO DI
3
H E TRAPANI DOMENICO DI
3 G
G
ANNO SCOLASTICO 2006/2007
GRUPPO DI LAVORO AMODEO DARIO, SCARAMOZZINO GIUSEPPE E ZAMINGA
SAMUELE DI
3 H E TRAPANI DOMENICO DI
3
H E TRAPANI DOMENICO DI
3 G
G
- EQUAZIONE DELLA CIRCONFERENZA;
- PROBLEMI SULLA CIRCONFERENZA;
La circonferenza,la parabola,l'ellisse e l'iperbole sono dette coniche poiché si possono ricavare dall'intersezione di un piano con due coni posti come una clessidra.
-CIRCONFERENZA
La circonferenza è l'insieme dei punti del piano equidistanti da un punto fisso detto centro ed è la sezione orizzontale di una clessidra.
Coniderando:
PC=r Il segmento PC è il raggio della
circonferenza.
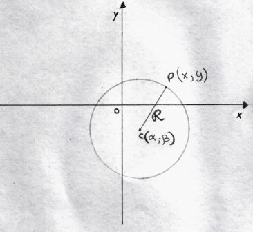
Eguagliamo la formula per calcolare il raggio,ossida la distanza
del
centro C dal punto P ed il raggio

Eleviamo entrambi i termini al quadrato e svolgiamo i quadrati interni alla radice ed abbiamo:

Ponendo:
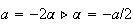
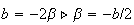
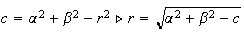
Abbiamo che:
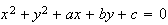 EQUAZIONE GENERALE DI UNA CIRCONFERENZA
EQUAZIONE GENERALE DI UNA CIRCONFERENZA
Sapendo l'equazione di una circonferenza possiamo calcolare le coordinate del centro C tramite formule inverse.
ESEMPIO:
Se abbiamo un'equazione del tipo
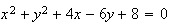 possiamo sapere che il centro C ha coordinate
possiamo sapere che il centro C ha coordinate
C(-2;3)
_ E che il raggio è
r =
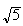 .
.
Queste sono le condizioni affinché un'equazione di 2° grado sia un'equazione di una circonferenza:
1. I due termini di secondo grado devono avere lo stesso coefficiente.
2. Manca il termine in xy.
3. La quantità α²+β²-c non deve essere negativa.
Invece queste sono le caratteristiche generali:
* Se manca il termine ax,il centro si trova sull'asse delle y;
* Se manca il termine by,il centro si trova sull'asse delle x;
* Se manca il termine c,la circonferenza passa per l'origine O;
* Se mancano i termini ax e by,il centro si trova sull'origine;
* Se mancano i termini ax e c,la circonferenza passa per l'origine O e ha il centro sull'asse y ed è tangente all'asse x;
* Se mancano i termini bx e c,la circonferenza passa per l'origine O e ha il centro sull'asse x ed è tangente all'asse y.
-Una circonferenza di equazione x²+y²=1 è detta goniometrica poiché ha il centro in O ed ha il raggio uguale a 1.
- PROBLEMI SULLA CIRCONFERENZA
 Come trovare l'equazione della circonferenza passante per tre punti assegnati
Come trovare l'equazione della circonferenza passante per tre punti assegnati
Per tre punti non allineati passa una ed una sola circonferenza.
Date le coordinate di tre punti vogliamo risalire all'equazione della circonferenza (naturalmente il problema si puo anche risolvere geometricamente) Per semplicita' risolviamo il problema su un esempio pratico
Trovare l'equazione della circonferenza passante per i punti

A(1;3) B(6;1) C(5;4)
Prendo l'equazione generica della circonferenza
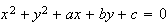
* Prima condizione: passaggio per A=(1,3)
Sostituisco le coordinate nell'equazione della circonferenza




* Seconda condizione: passaggio per B=(6,1)
Sostituisco le coordinate nell'equazione della circonferenza



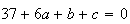
* Terza condizione: passaggio per C=(5,4)
Sostituisco le coordinate nell'equazione della circonferenza




Le tre condizioni devono valere contemporaneamente; faccio il sistema


troviamo i valori di a di b e di c:

sostituiamo a e avremo:


sviluppiamo i calcoli:


sostituiamo b e avremo:


sostituiamo i valore di c così da trovare b e a:


avendo i valori di a b e c posiamo scrivere l' aequazione della circonferenza che passa da quei punti che sarà:

 Come scrivere l'equazione della circonferenza di centro il punto C(2, -3) e
passante per il punto P =(-1,1).
Come scrivere l'equazione della circonferenza di centro il punto C(2, -3) e
passante per il punto P =(-1,1).
Risoluzione
In questo caso il raggio non è dato direttamente, ma si calcola immediatamente come distanza tra due punti.

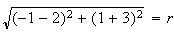


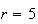
L'equazione della circonferenza si ottiene sostituendo nella generica equazione le coordinate del centro ed il valore di r e sviluppando i calcoli:
Dato che non sappiamo
che:

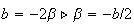
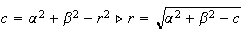
possiamo determinare subito a b e c dell' equazione della circonferenza quindi:
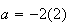
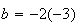

Allora l' equazione della circonfeenza sarà :
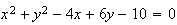
Come determinare l' equazione della circonferenza noti due punti
A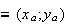 B
B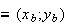 appartenenti alla circonferenza e l'equazione della retta r che contiene il
centro
appartenenti alla circonferenza e l'equazione della retta r che contiene il
centro
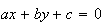
A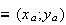
B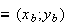
r: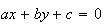
per prima cosa bisogna determinare l' equazione della corda ab mediante il
calcolo dell' equazione generale di un retta:
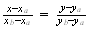
sviluppando i calcoli bisognerà pervenire all equazione in forma implicdita della quale si determineranno le coordinate del punto medio M
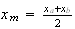
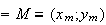
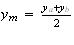
si trova la perpendicolare alla corda ab condotta dal punto
medio m l'asse dell corda ab

dove m è il coefficente angolare dell' equazione della corda e K è il termine noto che si detemina sostituendo a x e a y rispettivamente l' ascissa e l' ordinata del punto medio m
a questo punto si dovrà mettere a sistema l' equzione dell' asse di ab con la retta r al fine di determinare le coordinate del centro
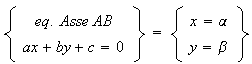
note le coordinate del centro si troveranno a, b, c, termini dell equazione della circonferenza che si ricavno dai passagg della dimostrazione dell' equainone della circonferenza
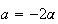
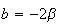
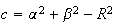
si potrà scrivere di conseguenza l' equazione della circonferenza pasante
per i punti
A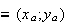 B
B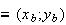 .
.